Over time financial market relationships evolve and change. These changes, or shifts, can have significant impact on the expected risk and returns of various investments. Traditional risk measures, such as volatility, correlation and betas, have fallen short in timely identification of these shifts. This paper focuses on a new and more scientific way of identifying these shifts in financial conditions and market dynamics.
Allocating capital in a changing financial world
Economic history is replete with fads and phases, eras and epochs of growth and inflation and the rise and fall of theories and policies. Markets have responded with bubbles and crashes, while the invisible hand did battle with the not-so-invisible boot of government policies. The changes that have spread through the world economy in the last few centuries have also led to identifiable regimes of behaviour. To assume that the immediate past, or even the past of a few decades, is the natural stationary state of markets is falling prey to recency bias; just because things have been a certain way recently does not mean they will stay the same. Yet this assumption is often baked in, implicitly but deeply, most risk management and monitoring tools, and also plays a large role in the framing of economic discussions and market outlooks. We need to disenthrall ourselves from this bias, and do so in a systematic and disciplined manner.
The investment challenge is to monitor and understand the changing financial landscape and allocate capital accordingly. Shifts in market behaviour where relationships change or no longer hold, which we would describe as a regime shift, provide significant challenges to asset allocation.
As asset allocators we constantly monitor a large range of risk measures and indicators with turbulence and absorption being two measures of capital market structure.
Do you have the time?
Markowitz’s (1952) pioneering work in modern portfolio theory provided investors a more scientific way to determine their asset allocation based on long-term assumptions around equilibrium expected returns, volatilities and correlations. Over long timeframes, this has served investors well; although as John Maynard Keynes puts it, “But this long run is a misleading guide to current affairs. In the long run we are all dead. Economists set themselves too easy, too useless a task, if in tempestuous seasons they can only tell us, that when the storm is long past, the ocean is flat again.” So we can’t dismiss the short-to-medium term or sequencing risks. While there is clearly no silver bullet, a “set-and-forget” asset allocation approach often falls short due to the timing of harmful capital market events relative to a particular investor’s time horizon.
So the pertinent question: is there a better way to achieve more consistent outcomes than relying on equilibrium assumptions and time diversification? First Sentier Investors (2014) provided a Dynamic Asset Allocation (DAA) framework that takes a shorter-term horizon than Strategic Asset Allocation (SAA) reallocating capital as investment markets evolve based on fundamental investment rationales. This paper focuses on non-traditional risk management measures that can inform both the SAA and DAA investment processes.
Risk is evolutionary, not stationary
The traditional measures of risk, such as betas, volatilities, correlations and value-at-risk, provide forward-looking or historical point estimates of portfolio characteristics. These measures arm the investor with estimates of the potential return distributions and asset class interactions. These risk metrics are extremely useful in the identification and assessment of unwanted portfolio features. This allows investors to tailor exposures to their risk appetite. However, these metrics are sensitive to the (generally historical) inputs. Large changes in the input assumptions can have a meaningful impact on the results and resulting interpretations, or indeed if the future is unlike the past.
The chart below illustrates how risk measures, in this case correlation, can vary over time. The historical correlation since 1990 between global equities and implied volatility (VIX index) is -0.53. Although the average historical volatility is intuitive, the variation is not. Indeed, adding a long position in volatility, which is typically used as a form of insurance, to reduce investment risk would not be warranted based on the positive correlations that occurred in December 1995 and January 2018 between global equities and implied volatility.
Figure 1: Global Equities vs Implied Volatility (VIX)
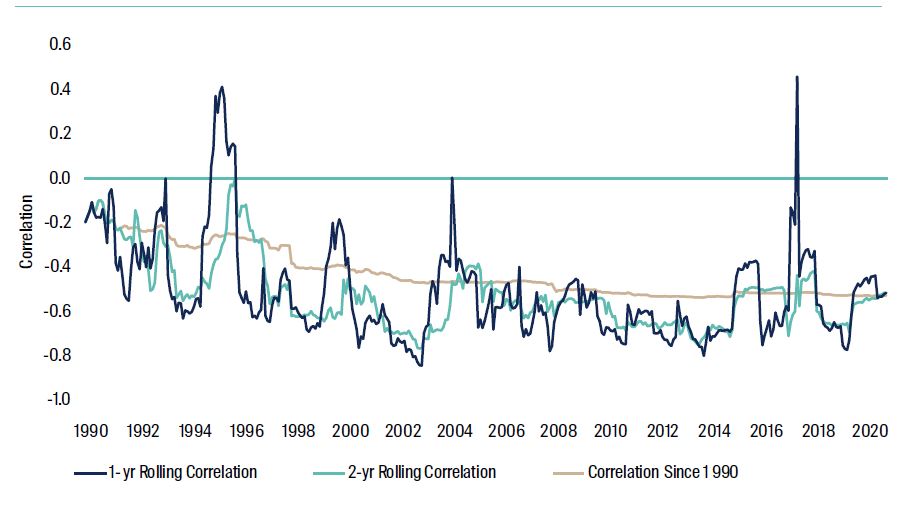
Source: Bloomberg, Internal Propriety Models. Data to 30 June 20211.
Another nuance with correlations is that they exhibit asymmetry. There is a large body of evidence2 showing that downside correlations for equity markets are much higher than upside correlations. Longin and Solnik (2001) show that for extreme movements, which focuses on the tails of the return distribution, large negative movements result in a much higher correlation than large positive movements. This (somewhat) erodes the rationale for portfolio diversification; sorry Markowitz3.
Although time-varying correlations and volatilities might provide a challenge to the traditional risk models, they do provide DAA opportunities. Ang and Bekaert (2002) evidenced the benefits of dynamically hedging foreign exchange exposure and introducing a risk-free asset into the portfolio as correlations and volatilities increase. The rationale for dynamic reallocation of capital is reinforced by Longin and Solnik’s (2001) findings that correlation asymmetries are exacerbated amongst small capitalisation, value and negative momentum stocks.
The benefit of being able to identify changes over time in capital markets should be higher risk- adjusted returns, through increased return potential and the preservation of capital. If we believe that we are experiencing ‘normal’ or ‘average’ capital market behaviour, then we may be able to rely on long-term historical averages or expected equilibriums. However, long-term allocations are highly likely to be suboptimal if we are not experiencing ‘normal’ capital market conditions.
Which ‘normal’? Old normal, new normal or abnormal?
A significant challenge to portfolio construction and risk management is the concept of regime shifts. For example a shift could be caused by unanticipated changes in growth, inflation, monetary policy, regulation, brittleness of the financial system or other secular shifts. The challenge for investors is to be able to identify regime shifts and determine the appropriate action, which could be a conscious decision of no-action.
Any shift in market conditions, especially a regime shift, has significant consequences for investors’ optimal portfolio allocation.
Goldfeld and Quandt (1973) suggested a Markov switching regression to characterise changes in parameters of an autoregressive process which Hamilton (1989) later applied to the US business cycle. These early insights have been further refined as the applications are wide ranging in financial markets.
Regime shifts result in different asset returns, volatilities and asset correlations (not to mention autocorrelations). To help us monitor regime shifts, we first need to determine an appropriate measure of abnormality in data or process for the identification of outliers. Mahalanobis (1927, 1936) defined a distance measure that was prompted by the requirement to compare the similarities, or lack thereof, of human skulls. We use this measure to calculate the degree of uncharacteristic behaviour within financial markets, capturing extreme price movements and changing relationships. Kritzman and Li (2010) coined the application of this measure to financial markets ‘Turbulence’4. We believe this represents an appropriate and vernacularly intelligible description of the distance measure when applied to financial markets and will refer to the Mahanlaobis distance as turbulence for the remainder of the paper.
As the foreign exchange market is the world’s largest and most liquid market it provides a great lens to view historical events. So when have we observed financial turbulence in foreign exchange markets? As we can see, turbulence in foreign exchange markets could be seen during the major events of: global recession of 1982, British government being forced to withdraw the pound sterling from the ERM, Swiss National Bank removing the floor against the euro, and the Global Financial Crisis.
Figure 2: Foreign Exchange Monthly Turbulence
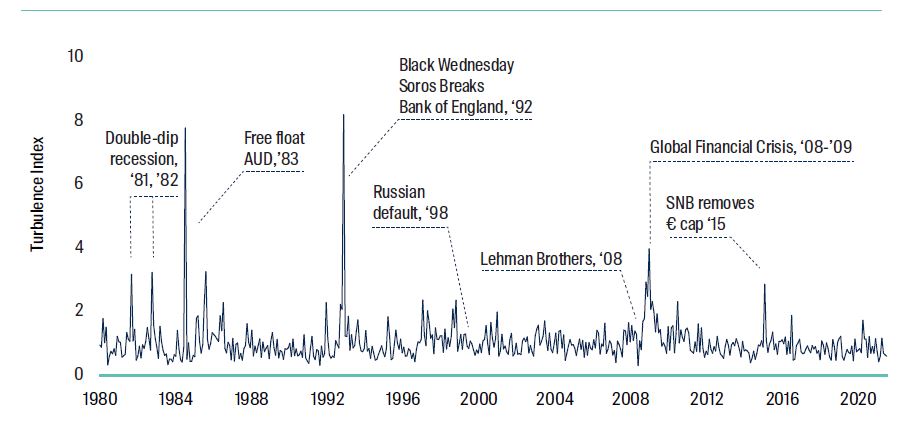
Source: Bloomberg, Internal Propriety Models. Data to 30 June 2021.
Although historical identification of crises is informative, it would be more useful to identify when a regime shift occurs. This allows for a timely review of any assumptions, such as volatilities and correlations, and the resulting allocations. A portfolio built on average market assumptions will become inappropriate when market behaviour changes.
We now focus on the identification of regime shifts. The aim is to remove the noise and change the information content to a probabilistic interpretation of market behaviour. This is helpful for two reasons: identifying when market behaviour is no longer ‘normal’, and secondly, to identify when markets return to normal.
To determine foreign exchange regimes we apply a two-state hidden Markov model to the foreign exchange turbulence. A four-state model is proposed by Guidolin and Timmermann (2006) to model the economic cycle of crash, recovery, slow growth, and bull. We acknowledge that a two-state model could oversimplify the behaviour of financial markets, although given the options of simple or complex we recognise Occam’s razor5.
Figure 3: Foreign Exchange Regimes
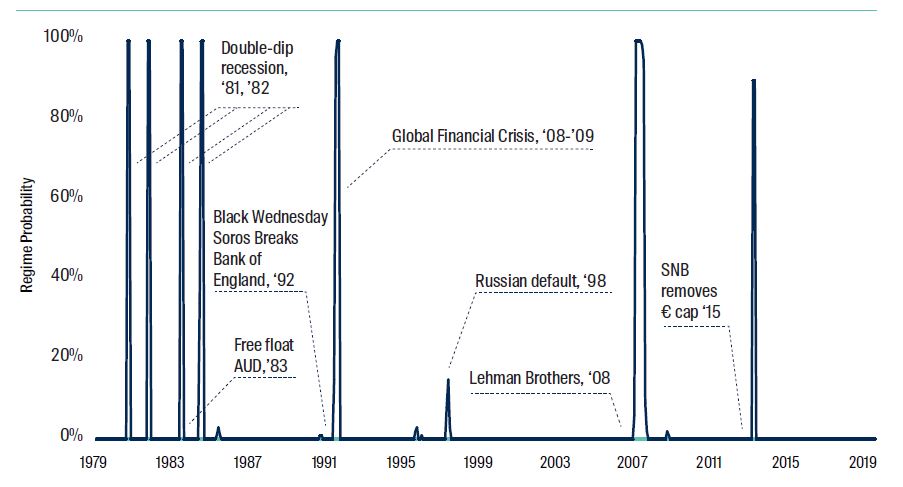
Source: Bloomberg, Internal Propriety Models. Data to 30 June 2021.
Posit that market activity can be characterised at any point in time as being in either one of two states: stable with low volatility, or alternatively fragile, with corresponding lower average return and higher volatility6. This is the basis for our two-state model with the first state being ‘normal’ and the second state being ‘ex-normal’.
The chart provides the graphical probabilities, where a probability of 0 indicates 100% likelihood of being in the ‘normal’ regime and value of 1 indicates 100% likelihood of being within ‘ex-normal’ regime.
This matches our view of market participants’ behaviour. For the most part market participants act rationally and try to maximise their risk-adjusted returns. However there are times where high emotions take control – leading to large scale panic. If we identify these shifts, then the challenge is to identify the allocations or positions that would perform well in the new environment, and to do so in a timely manner.
It is important to recognise that turbulence is not designed to identify cheap vs. rich valuations in asset markets. Valuation is a very different topic from changing market behaviour and we should not conflate the two. So far we have only investigated foreign exchange regimes. The benefit can be extended to equities, commodities, sovereign bonds, as well as investment subsectors and indeed even market factors, such as those identified by Fama and French.
Contagion: are my exposures unified or diversified?
In a utopian investment world we would be able to identify all the factors that drive our potential performance and risks. This would provide us with a much better macro level view of our ex-ante risk decomposition. Many investors have had the right thesis but the wrong positions.
The holy grail of asset allocation is the identification of uncorrelated compounding assets. So being able to find uncorrelated return and risk drivers would be significantly meaningful. Or in a risk context, the reverse would be informative: how unified are my exposures?
Numerous studies have published suggested measures of financial integration or segregation7. For example Forbes and Rigobon (1999) investigate shifts in the variance-covariance matrix to test for contagion whereas Eiling and Gérard (2007) calculate the extent of integration using global and regional factors. Pukthuanthong and Roll (2009) put forward an R-squared integration measure by regressing country returns on prior calendar year’s principal components.
We use principal components analysis (PCA) to decompose the variation in returns into uncorrelated factors that explain as much of the variation in returns as possible. This quantifies the degree to which performance is explained by the first n factors. Kritzman et al. (2011) used the moniker of ‘Absorption’ to describe the application of PCA to financial market returns. We prefer ‘brittleness’ as a more intuitive description although we retain ‘absorption’ to align terminology. The quantum these n factors can explain is called the absorption ratio. As the absorption ratio increases capital markets become more fragile, increasing the likelihood of shocks propagating through markets as fewer factors drive returns.
As the absorption ratio declines capital markets become more resilient, implying that isolated shocks are less likely to cascade and become terminal. In the illustration below we see how much the first two factors are driving the asset returns and ultimate risks.
Figure 4: Global Assets Brittleness - 5 & 10 Factors
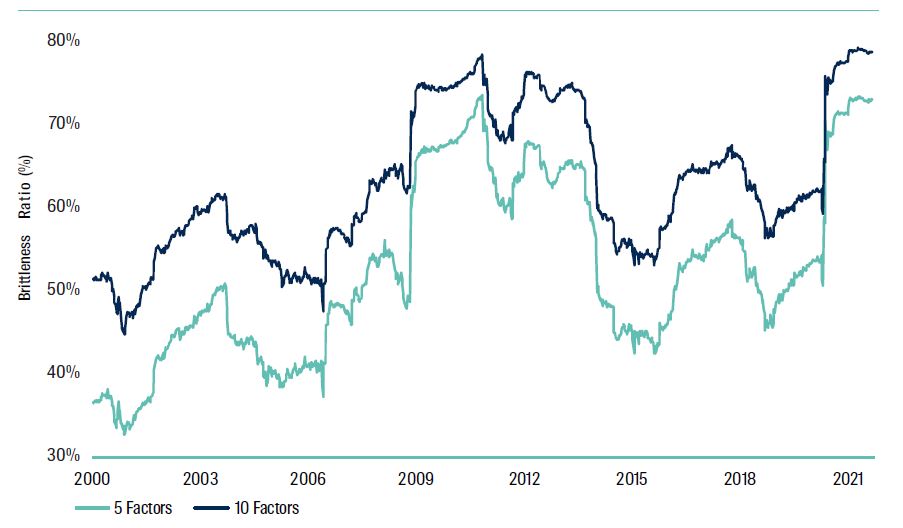
Source: Bloomberg, Internal Propriety Models. Data to 30 June 2021.
Taking the absorption ratio we again use regime shifts to provide us with a quantitative measure of the unification of financial markets. This provides us with another layer of capital market information. It also allows us to identify a number of historical events. When capital markets become coupled, broad portfolio protection strategies and tail risk strategies are likely to become meaningful. In the eye of the storm everything becomes a burden (or saviour in the case of insurance).
Figure 5: Global Assets Probability - 5 Factors
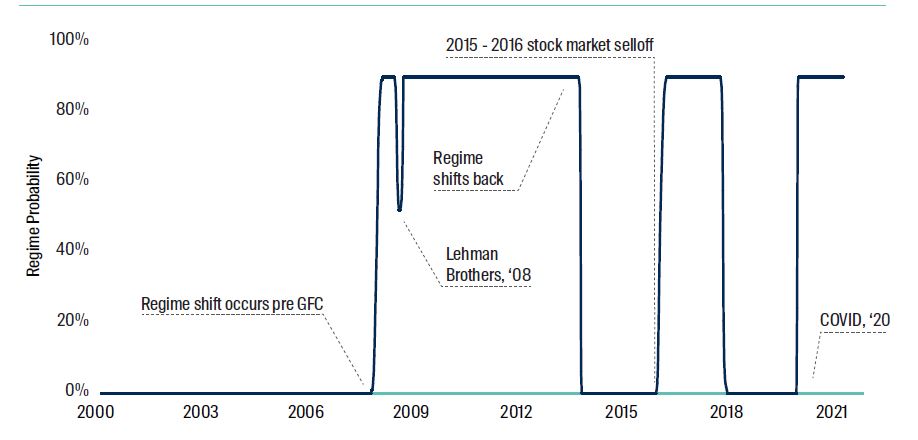
Source: Bloomberg, Internal Propriety Models. Data to 30 June 2021.
Why do we care?
Whilst there may be strong fundamental reasons underlying an investment thesis, at times the macro environment is going to dominate. Momentum can grow, cheap assets can get cheaper, and expensive assets can continue to rise in value. It is very difficult to design a portfolio based on irrational behaviour, although, it is possible to ensure that it is resilient.
The reason why we monitor turbulence and brittleness is to capture an additional dimension of risk. As asset allocators we closely monitor valuations, carry, momentum and other meaningful inputs such as supply and demand; central bank action and the political landscape to name a few. But these are only useful if we can understand them in the current market context.
- Global Equities is the MSCI World in USD. Implied Volatility is the CBOE SPX Volatility Index in USD.
- See Lin, Engle, and Ito (1994), Karolyi and Stulz (1996), Bae, Karolyi and Stulz (2000), Ang and Chen (2002).
- If future asset returns and co-variances need to be estimated, with an error term, then it follows that investors that underestimate the extent of co-movements will have greater risk than intended.
- Turbulence is calculated as Mahalanobis distance of recent sets of returns compared to their history.
- Occam’s razor is a problem-solving principle that gives precedence to simplicity; among competing hypotheses, the one with the fewest assumptions should be selected.
- Strictly speaking, the two states could also correspond to “higher average with higher volatility,” and “lower average with lower volatility,” although this is less common. The determination is done by the two-state hidden Markov model.
- Segregation being the opposite of integration.
Ang, A., & Bekaert, G. (2002). International asset allocation with regime shifts.
Review of Financial Studies, 15(4), 1137-1187. https://doi.org/10.1093/rfs/15.4.1137
Ang, A., & Chen, J. (2002). Asymmetric correlations of equity portfolios.
Journal of Financial Economics, 63(3), 443-494. https://doi.org/10.1016/s0304-405x(02)00068-5
Bae, K., Karolyi, G. A., & Stulz, R. (2000).
A new approach to measuring financial contagion. https://doi.org/10.3386/w7913
Eiling, E., & Gerard, B. (2011). Dispersion, equity returns correlations and market integration.
SSRN Electronic Journal. https://doi.org/10.2139/ssrn.891115
First Sentier Investors. (2014). “Dynamic Asset Allocation”.
Forbes, K., & Rigobon, R. (1999). No contagion, only interdependence:
Measuring stock market Co-movements. https://doi.org/10.3386/w7267
Goldfeld, S. M., & Quandt, R. E. (1973). A Markov model for switching regressions.
Journal of Econometrics, 1(1), 3-15. https://doi.org/10.1016/0304-4076(73)90002-x
Guidolin, M., & Timmermann, A. G. (2006). Asset allocation under multivariate regime switching.
SSRN Electronic Journal. https://doi.org/10.2139/ssrn.940652
Hamilton, J. D. (1989). A new approach to the economic analysis of Nonstationary time series and the business cycle.
Econometrica, 57(2), 357. https://doi.org/10.2307/1912559
Karolyi, G. A., & Stulz, R. (1996). Why do markets move together? An investigation of U.S.-Japan stock return Comovements using ADRS.
SSRN Electronic Journal. https://doi.org/10.2139/ssrn.40556
Kritzman, M., & Li, Y. (2010). Skulls, financial turbulence, and risk management.
Financial Analysts Journal, 66(5), 30-41. https://doi.org/10.2469/faj.v66.n5.3
Kritzman, M., Li, Y., Page, S., & Rigobon, R. (2010). Principal components as a measure of systemic risk.
SSRN Electronic Journal. https://doi.org/10.2139/ssrn.1633027
Lin, W., Engle, R. F., & Ito, T. (1994). Do bulls and bears move across borders? International transmission of stock returns and volatility.
Review of Financial Studies, 7(3), 507-538. https://doi.org/10.1093/rfs/7.3.507
Longin, F., & Solnik, B. (2001). Extreme correlation of international equity markets.
The Journal of Finance, 56(2), 649-676. https://doi.org/10.1111/0022-1082.00340
Mahalanobis, P.C. Analysis of Race-Mixture in Bengal,
Journal of the Asiatic Society of Bengal, vol. 23 (1927): 301–333.
Mahalanobis, P.C. On the Generalised Distance in Statistics,
Proceedings of the National Institute of Sciences of India, vol. 2, no. 1 (1936): 49–55.
Markowitz, H. (1952). Portfolio selection.
The Journal of Finance, 7(1), 77. https://doi.org/10.2307/2975974
Pukthuanthong, K., & Roll, R. (2009). Global market integration: An alternative measure and its application.
Journal of Financial Economics, 94(2), 214- 232. https://doi.org/10.1016/j.jfineco.2008.12.004
Important Information
This material has been prepared and issued by First Sentier Investors (Australia) IM Ltd (ABN 89 114 194 311, AFSL 289017) (Author). The Author forms part of First Sentier Investors, a global asset management business. First Sentier Investors is ultimately owned by Mitsubishi UFJ Financial Group, Inc (MUFG), a global financial group. A copy of the Financial Services Guide for the Author is available from First Sentier Investors on its website.
This material contains general information only. It is not intended to provide you with financial product advice and does not take into account your objectives, financial situation or needs. Before making an investment decision you should consider, with a financial advisor, whether this information is appropriate in light of your investment needs, objectives and financial situation. Any opinions expressed in this material are the opinions of the Author only and are subject to change without notice. Such opinions are not a recommendation to hold, purchase or sell a particular financial product and may not include all of the information needed to make an investment decision in relation to such a financial product.
To the extent permitted by law, no liability is accepted by MUFG, the Author nor their affiliates for any loss or damage as a result of any reliance on this material. This material contains, or is based upon, information that the Author believes to be accurate and reliable, however neither the Author, MUFG, nor their respective affiliates offer any warranty that it contains no factual errors. No part of this material may be reproduced or transmitted in any form or by any means without the prior written consent of the Author.
Get the right experience for you
Your location :  Australia
Australia
Australia & NZ
-
 Australia
Australia -
 New Zealand
New Zealand
Asia
-
 Hong Kong (English)
Hong Kong (English) -
 Hong Kong (Chinese)
Hong Kong (Chinese) -
 Singapore
Singapore -
 Japan
Japan























 United Kingdom
United Kingdom 