At AlbaCore, we focus on the long-term. As one of Europe’s leading alternative credit specialists, we invest in private capital solutions, opportunistic and dislocated credit, and structured products.
Discover moreInvestment strategies
Insights
Specialist in Asia Pacific, China, India and South East Asia and Global Emerging Market equities.
Discover more
Our philosophy is very simple. We are constantly searching for high quality businesses and when we acquire them, we will work relentlessly with them to create long-term sustainable value through innovation, ESG-led and proactive asset management.
Discover moreInvestment strategies
Insights
formerly Realindex Investments
Leader in active quantitative equities across Australian equities, global equities, emerging markets and global small companies.
Backed by a unique blend of research, portfolio construction and risk management, focused on uncovering original insights and translating them into investment strategies that are active and systematic, aiming to generate alpha.
Discover moreInvestment strategies
Insights
At Stewart Investors, we believe in putting people first. Our investment world-view is of a series of partnerships – with each other, with our clients, with the companies we invest in, the people who buy their goods and services, and with the wider society in which we all live and work.
Discover more
This Rmarkdown workbook steps through some of the modeling we have done in relation to assessing some of aspects of the ‘Your Future Your Super’ (YFYS) proposal by the Treasury. It is intended to be illustrative. The assumptions are general, and can be adjusted by the user.
Assumptions
We impose some high-level assumptions on the asset allocation bands of a balanced fund (default MySuper option). These assumptions are largely consistent with the assumptions provided by the modeling conducted by the Conexus working group. We have used 7 asset classes, and for simplicity without a loss of generality, we have ignored sector tilts such as broad caps vs small caps or developed vs. emerging markets. This is also consistent with APRA’s benchmarking, which does not distinguish for small caps or emerging markets.
Table 1 shows our mean SAA assumptions for the 7 asset classes and our asset allocation band deviation assumptions. Asset allocation deviations can be due to changes to a fund’s SAA or shorter term TAA / DAA positioning. In these simulations below, we don’t make further assumptions for distinguishing between the two with AA deviations. That is, we assume fund risk comes from three sources: i) SAA, ii) AA deviations and iii) manager selection. However, we note that AA deviations due to changes in long term SAA will be incorporated in the APRA benchmarks, and thus not assessed for under-performance, but shorter term TAA will be assessed.
Table 1. Generic Asset Allocation Bands for MySuper default option
We make some long-term mean variance assumptions. These assumptions are based on long term views of growth assets, mid-risk assets and defensive assets.
Table 2. Asset class mean variance assumptions
We have simplified asset class correlations into the following five categories.
- Growth assets: Equities
- Mid assets: Property and Infrastructure
- Credit
- Govt Bonds (FI)
- Cash
We assume asset classes with categories, such as Australian vs International Equities, have a correlation of 0.8.
Table 3. Asset class correlation matrix
Furthermore, we have made some assumptions on manager selection tracking error. We have assumed no correlation between manager alpha and asset class beta, i.e. alpha is orthogonal to beta. We have assumed a small level of correlation between cross-asset manager alpha, between say Australian Equities and International Equities.
Table 4. Generic Manager Tracking Error Assumptions
Internal Functions
Here lies some internal functions we will use for our analysis.
###########################
# Functions
###########################
# Generate a random MySuper balanced fund
# check weights add to 1 and satisfies constraints
.genBalancedFund <- function(bfAssumptions) {
wts <- apply(bfAssumptions, 1, function(x) { runif(1, min = x[5], max = x[4]) })
wts <- wts / sum(wts)
# check to see if weights satisfy lower-upper bounds
if(sum(bfAssumptions$lower < wts) == nrow(bfAssumptions) && sum(bfAssumptions$upper > wts) == nrow(bfAssumptions))
return(wts)
else
.genBalancedFund(bfAssumptions)
}
# Calculate Marginal Contribution to Total Risk and Tracking Error
# notes: http://webuser.bus.umich.edu/ppasquar/shortpaper6.pdf
calcMarginalRisk <- function() {
fundWgts <- .genBalancedFund(bfAssumptions)
SAAWgts <- bfAssumptions$meanWts
names(SAAWgts) <- rownames(bfAssumptions)
# totWgts = static SAA + TAA + Manager Selection
totWgts <- c(SAAWgts, fundWgts - SAAWgts, fundWgts)
relWgts <- c(rep(0, length(SAAWgts)), fundWgts - SAAWgts, fundWgts)
# calculate total fund risk and tracking error
totalRisk <- sqrt(t(as.matrix(totWgts)) %*% covAssetMgr %*% as.matrix(totWgts))[1,1]
trackingError <- sqrt(t(as.matrix(relWgts)) %*% covAssetMgr %*% as.matrix(relWgts))[1,1]
# marginal contribution to total risk and relative risk
mcTR <- totWgts * t(as.matrix(totWgts)) %*% covAssetMgr / totalRisk
mcTE <- relWgts * t(as.matrix(relWgts)) %*% covAssetMgr / trackingError
return(list(mcTR=mcTR, mcTE=mcTE))
}
# Generate MySuper balanced fund returns
# where AA deviations to static SAA is randomized
.genReturns <- function(yearsToRetirement, alphaAssumption=rep(0,numAssets)) {
fundWgts <- sapply(1:yearsToRetirement, function(x) .genBalancedFund(bfAssumptions))
rets <- mvrnorm(n=yearsToRetirement, mu=meanAsset, Sigma=covAsset)
mgrAlpha <- mvrnorm(n=yearsToRetirement, mu=alphaAssumption, Sigma=covMgr)
fundRets <- diag(rets %*% fundWgts)
fundAlpha <- diag(mgrAlpha %*% fundWgts)
return(fundRets + fundAlpha)
}
# Calculate the dollar value at the end of the accumulation stage
# i.e. total amount for retirement
calcRetirement<- function(contributions, alphaAssumption=rep(0,numAssets)) {
rets <- .genReturns(length(contributions), alphaAssumption = alphaAssumption)
cumrets <- cumprod(1 + rets)
accum <- sum(contributions * rev(cumrets))
return(accum)
}
# The Probability of Failure in the Annual Performance Test
.pFailHurdle <- function(IR, TE, years, hurdle= -0.005) {
alpha <- IR * TE
alpha_se <- sqrt(TE^2/ years)
pnorm(hurdle, mean = alpha, sd = alpha_se, lower.tail = T)
} Modeling 1. The marginal contribution of Asset Allocation vs Manager Selection in Absolute Total Risk and Relative Tracking Error
We simulate 10,000 balanced funds based on the asset allocation bands in our assumptions. For each balanced fund, we estimate it’s total risk, tracking error and marginal contributions to total risk and tracking error.
We show that:
- Asset allocation contribution dominates Total Risk. Hence member outcomes is largely driven by a super fund’s asset allocation decisions.
- On average, manager selection accounts for 60% of peer risk (aka Tracking Error).
nsims <- 10000
# run simulations
sims <- lapply(1:nsims, function(x) calcMarginalRisk())
TR <- sapply(sims, function(x) x$mcTR)
TE <- sapply(sims, function(x) x$mcTE)
rownames(TR) <- colnames(covAssetMgr)
rownames(TE) <- colnames(covAssetMgr)
# average marginal contribution to risk
mcTable <- data.frame(`Marginal Contribution to Total Risk (%)` = round(apply(TR, 1, mean)*100, 2),
`Marginal Contribution to Tracking Error (bps)` = round(apply(TE, 1, mean)*10000,2))
kable(mcTable, caption = "Marginal Contributions to Risk") 
# % of the marginal contribution from SAA, AA deviations and Manager Selection
row.idx <- lapply(c("SAA", "AA Deviations", "Mgr Selection"), function(x) grep(x, rownames(TE)))
pctTR <- apply(TR, 2, function(x) sapply(row.idx, function(y) sum(x[y]) / sum(x)))
pctTE <- apply(TE, 2, function(x) sapply(row.idx[-1], function(y) sum(x[y]) / sum(x)))
rownames(pctTR) <- c("SAA", "AA Deviations", "Mgr Selection")
rownames(pctTE) <- c("AA Deviations", "Mgr Selection")
# plot the distributions
# marginal contributions of total risk
pctTR_l <- melt(t(pctTR))
colnames(pctTR_l) <- c("sims", "source", "contribution")
ggplot(pctTR_l, aes(x = contribution *100, fill = source)) +
geom_histogram(aes(y=..density..), bins = 100) +
geom_density(alpha=.2) +
facet_free(source~. , scales = "free") +
xlab("Percentage contribution to Total Risk (%)") + theme_classic() +
ggtitle("The Percentage Marginal Contribution of Total Risk")
# marginal contributions of tracking error
pctTE_l <- melt(t(pctTE))
colnames(pctTE_l) <- c("sims", "source", "contribution")
ggplot(pctTE_l, aes(x = contribution *100, fill = source)) +
geom_histogram(aes(y=..density..), bins = 100) +
geom_density(alpha=.2) +
facet_free(source~. , scales = "free") +
xlab("Percentage contribution to Tracking Error (%)") + theme_classic() +
ggtitle("The Percentage Marginal Contribution of Tracking Error (Peer Risk)")
Modeling 2. On the probabilities of meeting member retirement outcomes
Here, we examine the impact of asset allocation and manager selection in meeting member retirement outcomes. We make a simplistic assumption that a member meets their retirement outcomes if they are able to accumulate their contributions under an annual return of CPI + 4% consistently. For instance, a women earning $100,000 pa with 2% wage growth and 9.5% super contributions over a period of 20 years should accumulate up to $441,975 for her super. Let’s assume this to be the retirement goal.
We look at the probability our ‘generic balanced plans’ misses these objectives.
- Manager selection is not a key driver of member outcomes.
- Asset allocation drives whether a member meets its retirement outcomes.
# sample member information
salary <- 100000L
annualContributions <- salary * 0.095
wageGrowth <- 0.02
yearsToRetirement <- 20
contributions <- annualContributions * cumprod(rep(1+wageGrowth, yearsToRetirement))
# CPI + 4% benchmark
# where CPI assumed to be circa 2% pa
bench <- rep(0.06, length(contributions))
cumbench <- cumprod(1 + bench)
accumbench <- sum(contributions * rev(cumbench))
print(paste0("For an annual salary of ", salary, " with 9.5% super contribution and wage growth of ", wageGrowth, " over ", yearsToRetirement, " years, the benchmark accumulation is: ", accumbench))## [1] "For an annual salary of 100000 with 9.5% super contribution and wage growth of 0.02 over 20 years, the benchmark accumulation is: 441975.280155874"# simulate retirement outcomes under 3 manager selection scenarios
nsims <- 10000
outcomes <- list()
outcomes[["none"]] <- sapply(1:nsims, function(x) calcRetirement(contributions))
outcomes[["negative"]] <- sapply(1:nsims, function(x) calcRetirement(contributions, rep(-0.005, numAssets)))
outcomes[["positive"]] <- sapply(1:nsims, function(x) calcRetirement(contributions, rep(+0.005, numAssets)))
outcomes <- as.data.frame(outcomes)
pctOutcomes <- outcomes / accumbench - 1
# plot simulations
pctOutcomes_long <- gather(pctOutcomes, alpha, outcome, 1:3)
ggplot(pctOutcomes_long, aes(x = outcome * 100, fill = alpha)) +
geom_histogram(aes(y=..density..), bins=50) +
geom_density(alpha=.2) +
facet_free(alpha~., scales = "free_y") +
geom_vline(aes(xintercept=mean(pctOutcomes$positive)*100, col="red"), show.legend = F) +
geom_vline(aes(xintercept=mean(pctOutcomes$none)*100, col="green"), show.legend = F) +
geom_vline(aes(xintercept=mean(pctOutcomes$negative)*100, col="blue"), show.legend = F) +
xlab("Percentage over the CPI + 4 benchmark at end of accumulation") + theme_classic() +
ggtitle("The Distribution of Member Outcomes")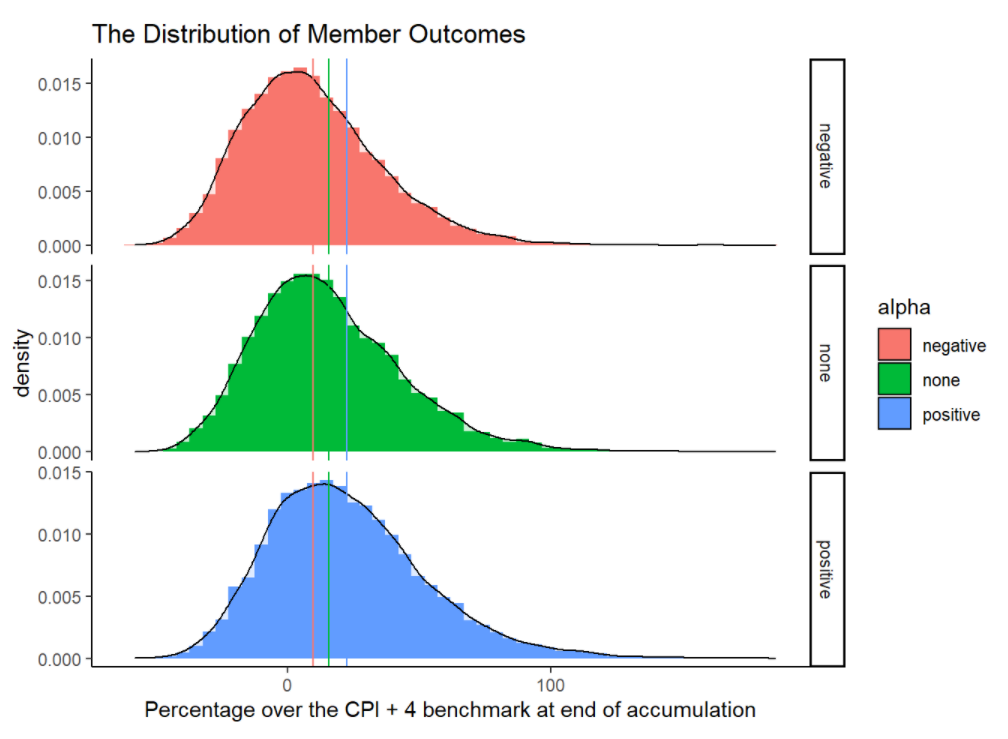
# percentage of outcomes that underperformed the CPI+4% benchmark
apply(pctOutcomes, 2, function(x) sum(x< 0) / length(x) )## none negative positive
## 0.3107 0.3952 0.2347Modeling 3. The Probability of Failure increases with Tracking Error
In this section, we examine how the annual performance test may incentivize index herding. We find that the probability of failure is reduced if funds choose to take less tracking error to the APRA benchmark returns. We show that at lower levels of tracking error, poor performance cannot be detected.
trackingErrors <-seq(0, 0.10, 0.001)
informationRatios <- seq(-0.5, +0.5, 0.01)
results <- matrix(0, length(trackingErrors), length(informationRatios))
rownames(results) <- trackingErrors * 100
colnames(results) <- informationRatios
for (i in 1:length(trackingErrors)) {
results[i, ] <- sapply(informationRatios, function(x) .pFailHurdle(x, TE = trackingErrors[i], years = 8))
}
levelplot(results,ylab = "Information Ratio", xlab = "Tracking Error (%)",
main = "Probability of Failure",
scales=list(x = list(at=seq(1, nrow(results),10)), y = list(at=seq(1, ncol(results),10))),
col.regions = colorRampPalette(rev(brewer.pal(4, "RdBu"))))
Modeling 4. Impact of Time Frame (Assessment Length) on False Positives
We test to examine if 8 years enough to assess a good fund from a bad fund. We find that at 8 years, most super funds would need to run at tracking errors of circa 1% or lower to be reasonably confident in not being accidently tested as an underperforming fund.
years <- seq(1,20, 1)
trackingErrors <- seq(0, 0.10, 0.005 )
results <- matrix(0, length(trackingErrors), length(years))
rownames(results) <- trackingErrors * 100
colnames(results) <- years
for (i in 1:length(trackingErrors)) {
results[i, ] <- sapply(years, function(x) .pFailHurdle(IR = 0, TE = trackingErrors[i], years = x))
}
levelplot(results,ylab = "Years", xlab = "Tracking Error (%)",
main = "Probability of Failure",
col.regions = colorRampPalette(rev(brewer.pal(4, "RdBu"))))
Disclaimer
This Workbook has been prepared by First Sentier Investors Realindex Pty Limited (ABN 24 133 312 017, AFSL 335381) (FSI RP) as a supplement to the publication titled “Addressing the Underperformance in Superannuation: Concerns around the Your Future, Your Super proposal” (Publication) and should only be read together with the Publication. The purpose of this Workbook is to illustrate the assumptions and the basis for the calculations that have been summarised in the Publication. It is not intended to provide financial product advice. The information, assumptions and the basis for the calculations herein are in the opinion of FSI RP accurate, reliable and reasonable, however neither FSI RP, Mitsubishi UFJ Financial Group, Inc (MUFG) nor their respective affiliates offer any warranty that such assumptions will eventuate or that the information or calculations contain no factual errors. To the extent permitted by law, no liability is accepted by MUFG, FSI RP nor their respective affiliates for any loss or damage as a result of any reliance on the information, assumptions or calculations in this Workbook.
 |  |
|---|